One Dimensional Monte Carlo Integration

我们要用两个章节的内容来讨论蒙特卡洛积分的相关知识

3.1 Expected Value

我们假设我们拥有以下所有条件：

1. a list of values $X$ that contains member $x_i$:

   \[X = (x_0, x_1, ..., x_{N-1})\]

2. a continous function $f(x)$ that takes members from the list:

   \[y_i = f(x_i)\]

3. a function $F(X)$ that takes the list $X$ as input and produces the list $Y$ as output:

   \[Y = F(X)\]

4. Where output list $Y$ has members $y_i$ :

   \[Y = (y_0, y_1, ..., y_{N-1}) = (f(x_0), f(x_1), ..., f(x_{N-1}))\]

有了上述这些条件，我们可以求得Y的算术平均值为：

\[\displaylines{\operatorname{average}(Y) = E[Y] = \frac{1}{N} \sum_{i=0}^{N-1} y_i \\ = \frac{1}{N} \sum_{i=0}^{N-1} f(x_i) \\ = E[F(X)]}\]

我们称$E[Y]$为$Y$的期望。

如果$x_i$的值是从一个连续区间$[a, b]$中随机选择的，那么我们有$a\le x_i \le b$对所有$i$成立，则$Y$的期望就可以近似为连续函数$f(x’)$在连续区间$[a, b]$上的平均值，即：

\[\displaylines{E[f(x') | a \leq x' \leq b] \approx E[F(X) | X = \{\small x_i | a \leq x_i \leq b \normalsize \} ] \\ \approx E[Y = \{\small y_i = f(x_i) | a \leq x_i \leq b \normalsize \} ] \\ \approx \frac{1}{N} \sum_{i=0}^{N-1} f(x_i)}\]

如果我们将N作为采样数量，同时取N的极限为$\infty$，则我们可以得到：

\[E[f(x') | a \leq x' \leq b] = \lim_{N \to \infty} \frac{1}{N} \sum_{i=0}^{N-1} f(x_i)\]

让我们总结一下，连续函数$f(x’)$在连续区间$[a, b]$上的期望值可以通过区间上无限数量的随机点采样并求和来表示。当采样数量趋近$\infty$时，采样之和的平均数就趋近于正确的答案。这就是蒙特卡洛算法。

但随机点采样也不是计算某个区间上的期望值的唯一方法，实际上我们也可以自己选择采样点的位置。如果我们在连续区间$[a, b]$上有N个采样点，那么我们可以距离均等地采样：

\[\displaylines{x_i=a + i\Delta x \\ \Delta x = \frac{b - a}{N}}\]

然后我们代入到计算期望的公式中，可得：

\[\displaylines{E[f(x') | a \leq x' \leq b] \approx \frac{1}{N} \sum_{i=0}^{N-1} f(x_i) \Big|_{x_i = a + i \Delta x} \\ E[f(x') | a \leq x' \leq b] \approx \frac{\Delta x}{b - a} \sum_{i=0}^{N-1} f(x_i) \Big|_{x_i = a + i \Delta x} \\ E[f(x') | a \leq x' \leq b] \approx \frac{1}{b - a} \sum_{i=0}^{N-1} f(x_i) \Delta x \Big|_{x_i = a + i \Delta x}}\]

再次取N的极限为$\infty$，则我们可以得到：

\[E[f(x') | a \leq x' \leq b] = \lim_{N \to \infty} \frac{1}{b - a} \sum_{i=0}^{N-1} f(x_i) \Delta x \Big|_{x_i = a + i \Delta x}\]

实际上，这就是一个常规积分的形式：

\[E[f(x') | a \leq x' \leq b] = \frac{1}{b - a} \int_{a}^{b} f(x) dx\]

我们又知道，积分在几何上的意义可以是函数曲线下的面积：

\[E[f(x) | a \leq x \leq b] = \frac{1}{b - a} \cdot \operatorname{area}(f(x), a, b)\]

接下里我们再通过一个例子来加强我们的理解

3.2 Integrating $x^2$

我们先来看下面这个积分

\[I = \int_{0}^{2} x^2 dx\]

使用常规方法，我们可以计算出

\[I = \frac{1}{3} (2^3 - 0^3) = \frac{8}{3}\]

如果使用蒙特卡洛方法计算积分，则我们有：

\[\displaylines{E[f(x) | a \leq x \leq b] = \frac{1}{b - a} \cdot \operatorname{area}(f(x), a, b) \\ \operatorname{average}(x^2, 0, 2) = \frac{1}{2 - 0} \cdot \operatorname{area}( x^2, 0, 2 ) \\ \operatorname{average}(x^2, 0, 2) = \frac{1}{2 - 0} \cdot I \\ I = 2 \cdot \operatorname{average}(x^2, 0, 2)}\]

我们用代码完成近似值的计算：

#include "rayTracing.h"

#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>

int main()
{
    int a = 0;
    int b = 2;
    int N = 1000000;
    double sum = 0.0;
    for (int i = 0; i < N; i++)
    {
        double x = randomDouble(a, b);
        sum += x * x;
    }
    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << (b - a) * (sum / N) << '\n';
}

3.3 Density Function

我们在rayColor函数，虽然简单且优雅，但是有一个巨大的问题：场景中使用小光源会带来大量的噪点，也就是我们会在深色像素周围看到很亮的像素。这是因为我们当前的均匀采样方法，对这样的光源来说采样频率不够高。只有当光线散射到光源所在的方向上时，才会对光源采样。对于小光源和距离较远的光源来说，这种弊端会尤为显著。

对于这个问题，我们有一个简单粗暴的解决办法。对于任意一个给定的光线，我们通常从相机开始追踪，然后光线穿过场景，最后终止于光源。如果我们反过来，从光源开始追踪光线，然后穿过场景，最后终止于相机，这种情况下，光线在开始时会有很强的亮度，然后会在场景中的连续反弹中失去能量，当光线到达相机时，它会被各种表面的反射变暗和着色。如果，我们迫使光源射出的光线尽快地反弹到相机上，这种做法也就等同于我们想光源发送更多的随机采样。但是这种光线会由于缺少连续的反射而最终具有不正确的亮度，虽然可以解决黑色像素旁有明亮像素的问题，但是也会使得所有像素变量。

有没有改进的方法呢？我们可以通过降低这些采样的权重来消除这种不正确的亮度的光线的影响，从而调节过度采样。但是具体的做法是怎样的呢？这时候我们需要引入新的概念：密度函数与概率密度函数

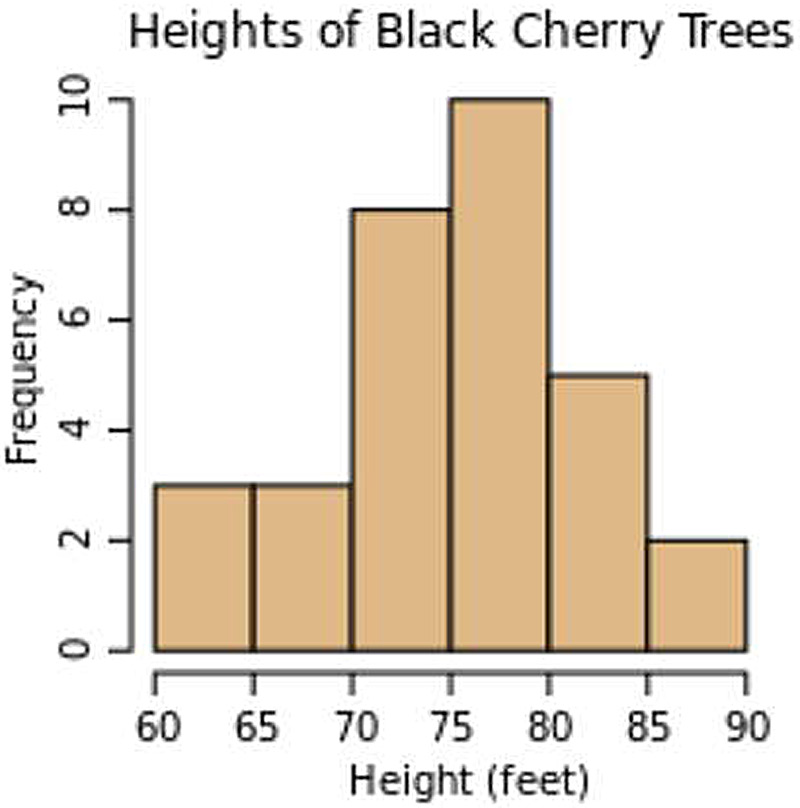
我们可以将密度函数理解为直方图的一种连续的版本。下面是一个直方图的实例：

在直方图中，如果将每个条形的数值范围减少，则条形的数目会变多，同时每个条形所对应的频率也会降低。如果我们将条形的数量增加到无穷，则我们将会有无限数量个的频率为零的条形。为了解决这个问题，我们可以使用离散密度函数来代替离散函数的直方图，它们之间的区别在于，离散密度函数将Y轴上的值归一化为总数的百分比，也就是密度，而不再是每个条形的计数。从离散函数转换到离散密度函数很简单：

\[\text{Density of Bin i} = \frac{\text{Number of items in Bin i}} {\text{Number of items total}}\]

一旦我们有了离散密度函数，我们就可以通过将离散值变更为连续值的方法，将离散密度函数转换为连续密度函数：

\[\text{Bin Density} = \frac{(\text{Fraction of trees between height }H\text{ and }H’)} {(H-H’)}\]

当我们想要知道某个树的高度时，我们可以构建一个概率函数，它能够告诉该树落在特定条形中的概率有多大：

\[\text{Probability of Bin i} = \frac{\text{Number of items in Bin i}} {\text{Number of items total}}\]

如果我们将概率函数和密度函数组合在一次，我们就可以将其解释为树高度的统计预测因子：

\[\text{Probability a random tree is between } H \text{ and } H’ = \text{Bin Density}\cdot(H-H’)\]

简而言之，概率密度函数（简称为PDF）是一个连续函数，可以对其进行积分以确定结果在积分上的可能性。

3.4 Constructing a PDF

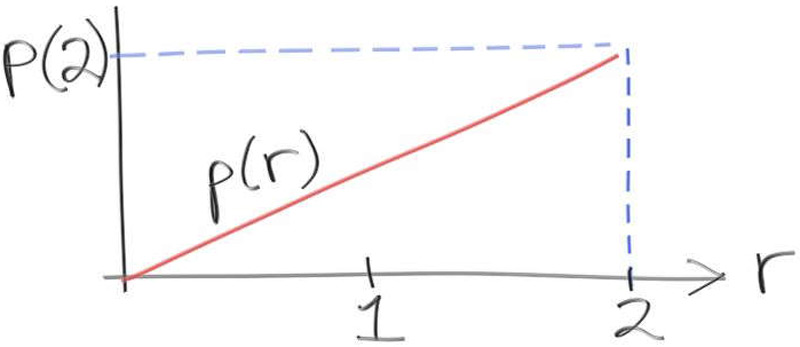
让我们使用下面这个函数来构建一个PDF

如果我们将$p(r)$作为一个PDF，根据PDF的性质，我们可得:

\[\operatorname{area}(p(r), 0, 2) = 1\]

同时，由于$p(r)$是一个线性函数，我们可以将其表示为常数乘以变量的形式，即

\[p(r)=C \cdot r\]

那么我们就可以通过积分来倒推常数$C$：

\[\displaylines{1 = \operatorname{area}(p(r), 0, 2) \\ = \int_{0}^{2} C \cdot r dr \\ = C \cdot \int_{0}^{2} r dr \\ = C \cdot \frac{r^2}{2} \Big|_{0}^{2} \\ = C ( \frac{2^2}{2} - \frac{0}{2} ) \\ C = \frac{1}{2}}\]

这样，我们就可以得到$r$在区间$[x_0, x_1]$上的概率为：

\[\operatorname{Probability} (r | x_0 \leq r \leq x_1 ) = \int_{x_0}^{x_1} \frac{r}{2} dr\]

此外，PDF作为一个连续函数，只能告诉你变量落在某个特定区间上的概率，当你想要计算区间某一个确切的值的概率时，得到的结果永远是0。

3.5 Choosing our Samples

如果我们已经有了对于一个特定函数的PDF，那么我们就可以计算出该函数在任意区间内取值的概率。这个性质在光线追踪中很重要，因为我们可以用PDF来确定在场景中的采样方式。如果场景中的PDF已知，那么我们就可以在保持场景亮度准确性的前提下，将更多的光线引导向光源。只是在研究这个问题之前，我们还需要解决如何使用PDF生成一个随机数的问题。

“生成具有PDF的随机数”，我们可以将这句话理解为：从一个特定的PDF所定义的分布中抽取随机样本。

比方说，我们有一个在区间$[0, 10]$上均匀分布的PDF，如果要使用这个PDF来生成随机数，那么随机数生成器就必须同样满足均匀生成随机值的条件。我们的光线追踪器所使用randomZeroToOne()就符合这个要求。所以，我们就可以通过10.0 * randomZeroToOne()在生成一个符合该PDF的随机数。

然而问题在于，大多数情况下，我们所关心的PDF都不是均匀的，所以我们需要通过某种方法，将均匀的随机数生成器，转换为非均匀的随机数生成器，且该随机数生成器的分布有PDF定义。

我们还是通过例子来思考，对于函数$p(r)=\frac{r}{2}$的在区间$[0, 10]$上的PDF，其中当值越接近于2时，概率越大。我们知道，必然存在一个值$x$，使得被该值分割的两个区间的概率相等，换句话说，任选一个值，则该值小于$x$与大于$x$的概率相等，都是50%。我们依然可以通过积分求解$x$：

\[50\% = \int_{0}^{x} \frac{r}{2} dr = \int_{x}^{2} \frac{r}{2} dr\]

解得：

\[\displaylines{0.5 = \frac{r^2}{4} \Big|_{0}^{x} \\ 0.5 = \frac{x^2}{4} \\ x^2 = 2 \\ x = \sqrt{2}}\]

让我们再次回顾一下我们的问题：如何使用均等的随机数生成器，生成符合非均匀PDF的随机数。有了$x=\sqrt2$，我们就可以创建一个新的函数f(d)，它使用double d = randomZeroToOne作为参数，如果d小于等于0.5，则返回一个范围在$[0, \sqrt2]$的随机数，否则返回一个范围在$[\sqrt2， 2]$的随机数：

double f(double d)
{
	if (d <= 0.5)
		return sqrt(2.0) * randomZeroToOne();
    else
        return sqrt(2.0) + (2 - sqrt(2.0)) * randomZeroToOne();
}

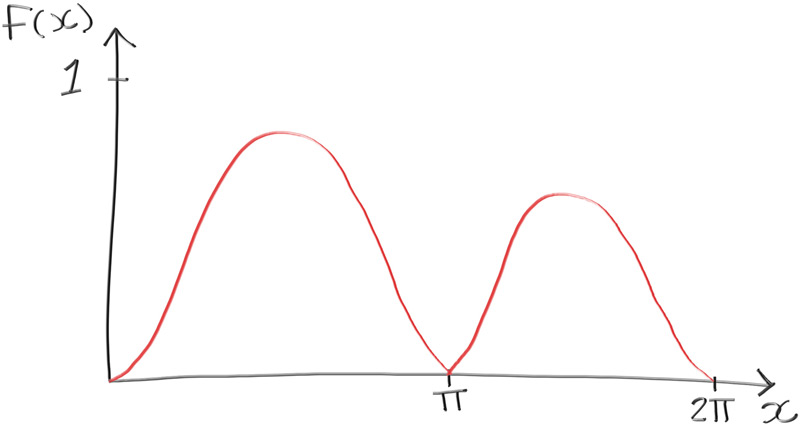
当然我们所举的列子是可以通过解析法计算的，相对来说比较简单。我们来看下面这个函数：

\[p(x) = e^{\frac{-x}{2 \pi}} sin^2(x)\]

函数图像如下：

#include "rayTracing.h"

#include <algorithm>
#include <vector>
#include <iostream>
#include <iomanip>
#include <math.h>
#include <cmath>
#include <stdlib.h>

struct sample
{
    double x;
    double pX;
};

bool compareByX(const sample& a, const sample& b)
{
    return a.x < b.x;
}

int main()
{
    unsigned int N = 10000;
    double sum = 0.0;
    
    // iterate through all of our samples
    std::vector<sample> samples;
    for (unsigned int i = 0; i < N; i++)
    {
        // get the area under the curve
        auto x = randomDouble(0, 2 * pi);
        auto sinX = sin(x);
        auto pX = exp(-x / (2 * pi)) * sinX * sinX;
        sum += pX;
        // store this sample
        sample thisSample = {x, pX};
        sample.push_back(thisSample);
    }
    
    // sort samples by x
    std::sort(samples.begin(), samples.end(), compareByX);
    
    // find out the samples at which we have half of our area
    double halfSum = sum / 2.0;
    double halfWayPoint = 0.0;
    double accum = 0.0;
    for (unsigned int i = 0; i < N; i++)
    {
        accum += samples[i].pX;
        if (accum >= halfSum)
        {
            halfWayPoint = samples[i].x;
            break;
        }
    }
    
    std::cout << std::fixed << std::setprecision(12);
    std::cout << "Average = " << sum / N << '\n';
    std::cout << "Area under curve = " << 2 * pi * sum / N << '\n';
    std::cout << "Halfway = " << halfway_point << '\n';
}